Statistical Learning
Statistical learning refers to a vast set of tools for understanding data. These tools can be classified as supervised or unsupervised.
- Supervised Statistical Learning involves building a statistical model for predicting, or estimating, an output based on one or more inputs . Problems of this nature occur in fields as diverse as business, medicine, astrophysics, and public policy.
- Unsupervised Statistical Learning involves inputs but no supervising output ; nevertheless we can learn relationships and structure from such data.
Supervised Learning
In machine learning, we generally refer to the act of estimating an element of the output space as prediction. To this end, in supervised learning the given data includes some elements (instances, observations) of the input space and their corresponding elements from the output space. There are two main types of supervised learning: classification and regression.
- Classification Problems: If the output space contains realizations of categorical random variables, the task is called classification, and the model is called classifier.
- Regression Problems: If the output space contains realizations of numeric random variables (continuous or discrete), the task is known as regression, and the model is called regressor.
Unsupervised Learning
In unsupervised learning, the data includes only a sample of the input space (realizations of some random variables): there is no known output. Here, the learning algorithm is just shown the input data and asked to extract knowledge from this data. We will look into two kinds of unsupervised learning in this chapter: dimensionality reduction and clustering.
- Dimensionality Reduction Methods: These methods take a high-dimensional representation of the data, consisting of many features, and finds a new way to represent this data that summarizes the essential characteristics with fewer features. A common application for dimensionality reduction is reduction to two dimensions for visualization purposes.
- Clustering Methods: Clustering partition data into distinct groups of similar items. The goal is to discover groups of similar observations within a given data.
A major challenge in unsupervised learning is evaluating whether the algorithm learned something useful. Most of the time is very hard to say whether a model did well. As a consequence, unsupervised algorithms are used often in an exploratory setting and as a preprocessing step for supervises algorithms.
Model Evaluation
The worth of a predictive model rests with its ability to predict. As a result, a key issue in the design process is measuring the predictive capacity of trained predictive models. This process, which is generally referred to as model evaluation or error estimation, can indeed permeate the entire design process.
In order to evaluate the performance of a statistical learning method on a given data set, we need some way to measure how well its predictions actually match the observed data. That is, we need to quantify the extent to which the predicted response value for a given observation is close to the true response value for that observation.
Idea: we do not really care how well the method works training on the training data. Rather, we are interested in the accuracy of the predictions that we obtain when we apply our method to previously unseen test data.
If a model is able to make accurate predictions on unseen data, we say it is able to generalize from the training set to the test set.
We want to build a model that is able to generalize as accurately as possible.
Overfitting, Underfitting
How can we go about trying to select a method that maximizes predictive performance on unseen data? One might imagine simply selecting a statistical learning method that minimizes the training MSE. This seems like it might be a sensible approach, since the training MSE and the test MSE appear to be closely related. Well, this is wrong.
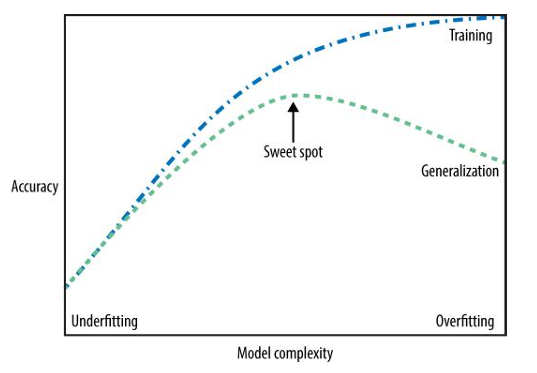
This is a fundamental property of statistical learning: As model flexibility increases, training MSE will decrease, but the test MSE may not. When a given method yields a small training MSE but a large test MSE, we are said to be overfitting the data.
Overfitting refers specifically to the case in which a less flexible model would have yielded a smaller test MSE.
We always want to find the simplest model. Building a model that is too complex for the amount of information we have, is called overfitting.
- Overfitting occurs when you fit a model too closely to the particularities of the training set and obtain a model that works well on the training set but is not able to generalize to new data.
- On the other hand, if your model is too simple, then you might not be able to capture all the aspects of and variability in the data, and your model will do badly even on the training set. Choosing too simple a model is called Underfitting.
The Trade-Off and the Sweet Spot
The more complex we allow our model to be, the better we will be able to predict on the training data. However, if our model becomes too complex, we start focusing too much on each individual data point in our training set, and the model will not generalize well to new data There is a sweet spot in between that will yield the best generalization performance. This is the model we want to find.